1 总体(太长不看版)
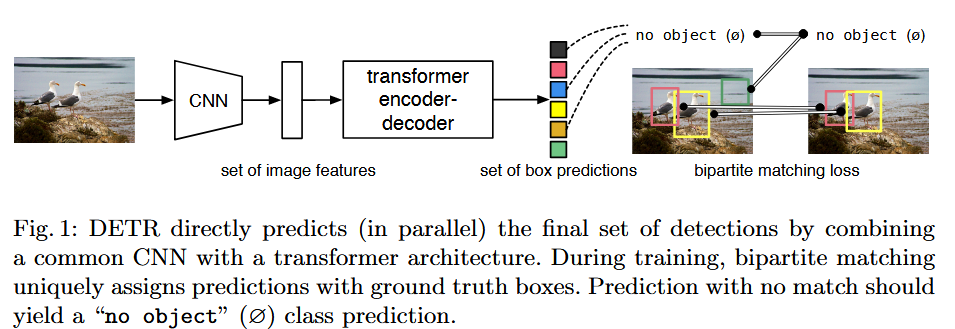
DETR的模型包括三部分:CNN backbone提取图像特征、transformer增强图像特征、FFN利用图像特征进行预测。DETR将目标检测视作是集合预测问题(set prediction problems),摒弃了传统方法中手工设计部分(如区域提议网络RPN、非极大值抑制NMS等,idk啊我不懂啊~~)。
DETR使用二分图匹配,设计了一个loss,并且设计了object query的embedding控制生成预测的数目。将每一个预测的边界框(class,boxes)与唯一一个真实物体框相对应,通过这种方法DETR可以实现端到端的检测框架(什么含金量啊~~)。且DETR结合了当下最流行的transformer架构,自注意力机制能够使模型更全面了解到图像的上下文和全局关系,从而增强模型的检测效果。
2 DETR的Loss
2.1 集合预测Loss
前提:假设我们知道DETR有N个object queries(N=100),可以预测得到100个边界框,而我们的GT物体也有N个(可能真实的GT只有几个,但最后被填充到N个,填充的类别即为"no object")。
(那么我们怎么知道哪个预测的边界框是和哪个GT框一一对应的的呢?)答案就是用二分图匹配,举个例子,假如矩阵的横纵轴分别是任务以及工人,其中的值是时间,每个工人只能去做一项任务且不同的工人必须做不同的任务,那么如何分配工人和任务才能使得时间成本最低就是二分图匹配要做的事儿。我们可以用暴力穷举,也可以用其他算法,此处论文使用了匈牙利算法。其中任务和工人分别是GT和预测,而矩阵的值则是论文设定的集合预测loss。
先梳理一下数据前提:
$$ \begin{aligned} y_i &= \langle c, b_i \rangle \text{ 为真实边界框的类别和boxes}\\ \hat{y_i} &= \langle \hat{c}, \hat{b_i} \rangle \text{ 为预测边界框的类别和boxes}\\ b_i &= \langle x, y, h, w \rangle \in [0,1] \text{ 表示boxes的中心坐标和相较于原图尺寸的H、W比例, 均归一化}\\ p &\text{ 为预测的类别经过softmax后得到的概率} \end{aligned} $$那么集合预测loss就为:
$$ \mathcal{L}_{\text{match}}(y, \hat{y}) = -\mathbb{1}_{\{c_i \neq \emptyset\}} \hat{p}_{\hat{\sigma}(i)}(c_i) + \mathbb{1}_{\{c_i \neq \emptyset\}} \mathcal{L}_{\text{box}}(b_i, \hat{b}_{\hat{\sigma}(i)}) $$新插入:
$$ \hat{fuck_{you}} = \frac{1}{2} $$ $$ \begin{Bmatrix} a & b \\ c & d \end{Bmatrix} $$而我们的目标就是找到这样一个matcher $\hat{\sigma}$ 使得最后cost matrix矩阵里的集合预测Loss总和最小。
$$ \hat{\sigma}= \underset{\sigma \in \mathfrak{S}_N}{\arg\min} \sum_{i=1}^{N} \mathcal{L}_{\text{match}}(y_i, \hat{y}_{\sigma(i)}) $$2.2 集合预测Loss源码解读
matcher.py/class HungarianMatcher
## class HungarianMatcher(nn.Module)的forward函数
@torch.no_grad()
def forward(self, outputs, targets):
bs, num_queries = outputs["pred_logits"].shape[:2] # outputs包含两个keys:pred_logits和pred_boxes
# 尺寸分别为(bs, num_queries, num_classes) ; (bs, num_queries, 4)
# We flatten to compute the cost matrices in a batch
out_prob = outputs["pred_logits"].flatten(0, 1).softmax(-1) # [batch_size * num_queries, num_classes]
out_bbox = outputs["pred_boxes"].flatten(0, 1) # [batch_size * num_queries, 4]
# Also concat the target labels and boxes
tgt_ids = torch.cat([v["labels"] for v in targets]) # target是个列表,有bs个值,值为字典(key为之前设计的annotation),取boxes和labels
tgt_bbox = torch.cat([v["boxes"] for v in targets]) # 注意如果一张image里有2个object,那么boxes和labels也就有2个值,分别表示这两个objects
# cat在一起,假如一共有6个objects,那么ids长度为[6],bbox长度为[6,4]
# Compute the classification cost. Contrary to the loss, we don't use the NLL,
# but approximate it in 1 - proba[target class].
# The 1 is a constant that doesn't change the matching, it can be ommitted.
cost_class = -out_prob[:, tgt_ids] # 假设该batch有共有6个objects,下面同,cost_class尺寸为[bs * num_queries, 6]
# Compute the L1 cost between boxes
cost_bbox = torch.cdist(out_bbox, tgt_bbox, p=1) # 计算L1距离,返回尺寸为[bs * num_queries , 6]
# Compute the giou cost betwen boxes
cost_giou = -generalized_box_iou(box_cxcywh_to_xyxy(out_bbox), box_cxcywh_to_xyxy(tgt_bbox))
# Final cost matrix
C = self.cost_bbox * cost_bbox + self.cost_class * cost_class + self.cost_giou * cost_giou # [200,6]
C = C.view(bs, num_queries, -1).cpu() # [bs,num_queries,6]
sizes = [len(v["boxes"]) for v in targets] # sizes尺寸为[bs],表示每一张图有多少个objects,此处为[2,4]
indices = [linear_sum_assignment(c[i]) for i, c in enumerate(C.split(sizes, -1))] # 将C沿最后一维,拆分成[bs,num_queries,2], [bs,num_queries,4]
# 返回的indices为[(array([22, 70], dtype=int64), array([0, 1], dtype=int64)), (array([ 7, 33, 34, 69], dtype=int64), array([0, 1, 2, 3], dtype=int64))]
# 可以用理解为第22个object query对应第一个图像的第0个object
return [(torch.as_tensor(i, dtype=torch.int64), torch.as_tensor(j, dtype=torch.int64)) for i, j in indices]

关于GIoU Loss
import torch
from torchvision.ops.boxes import box_area
def box_cxcywh_to_xyxy(x):
x_c, y_c, w, h = x.unbind(-1) #x为[200,4],最后一维unbind,得到4个[200]
b = [(x_c - 0.5 * w), (y_c - 0.5 * h),
(x_c + 0.5 * w), (y_c + 0.5 * h)] # 四个角坐标计算(左上角和右下角)
return torch.stack(b, dim=-1) #stack回去
# modified from torchvision to also return the union
def box_iou(boxes1, boxes2):
area1 = box_area(boxes1) #[200]
area2 = box_area(boxes2) #[6]
lt = torch.max(boxes1[:, None, :2], boxes2[:, :2]) # [bs*num_queries, 6, 2]
rb = torch.min(boxes1[:, None, 2:], boxes2[:, 2:]) # 比较bs*num_queries个预测框和 6个GT框的最多值,比如[1,6,2]指的是第一个预测框和所有GT框的左上角最大值/右下角最小值
wh = (rb - lt).clamp(min=0) # 交集区域内部的w和h
inter = wh[:, :, 0] * wh[:, :, 1] # [bs*num_queries, 6],表示交集面积
union = area1[:, None] + area2 - inter # [bs*num_queries, 6], 并集区域面积,
iou = inter / union # iou = 交集面积/并集面积
return iou, union
def generalized_box_iou(boxes1, boxes2):
"""
Generalized IoU from https://giou.stanford.edu/
The boxes should be in [x0, y0, x1, y1] format
Returns a [N, M] pairwise matrix, where N = len(boxes1)
and M = len(boxes2)
"""
# degenerate boxes gives inf / nan results
# so do an early check
assert (boxes1[:, 2:] >= boxes1[:, :2]).all() # 现在的boxes是左上角坐标(较小)和右下角坐标(较大)
assert (boxes2[:, 2:] >= boxes2[:, :2]).all()
iou, union = box_iou(boxes1, boxes2)
lt = torch.min(boxes1[:, None, :2], boxes2[:, :2])
rb = torch.max(boxes1[:, None, 2:], boxes2[:, 2:])
wh = (rb - lt).clamp(min=0) # [N,M,2]
area = wh[:, :, 0] * wh[:, :, 1]
return iou - (area - union) / area # giou = iou - (并集-交集)/并集
2.3 匈牙利Loss及源码
Loss公式如下:
$$ \mathcal{L}_{\text{Hungarian}}(y, \hat{y}) = \sum_{i=1}^{N} \left[-\log \hat{p}_{\hat{\sigma}(i)}(c_i) + \mathbf{1}_{\{c_i \neq \varnothing\}} \mathcal{L}_{\text{box}}(b_i, \hat{b}_{\hat{\sigma}(i)})\right] $$- 此处需要注意的是这里的label loss不在只是对非“no object"做,计算label loss之前会去填充target,填充值为91表示"no object",使之和预测boxes的尺寸一样[bs,num_queries]。
num_boxes = sum(len(t["labels"]) for t in targets) # [num_objects],此处为[6]
num_boxes = torch.as_tensor([num_boxes], dtype=torch.float, device=next(iter(outputs.values())).device)
if is_dist_avail_and_initialized():
torch.distributed.all_reduce(num_boxes)
num_boxes = torch.clamp(num_boxes / get_world_size(), min=1).item() # 检查每个gpu上的boxes是否小于1
# Compute all the requested losses
losses = {}
for loss in self.losses:
losses.update(self.get_loss(loss, outputs, targets, indices, num_boxes))
- label loss:
def loss_labels(self, outputs, targets, indices, num_boxes, log=True):
"""Classification loss (NLL)
targets dicts must contain the key "labels" containing a tensor of dim [nb_target_boxes]
"""
assert 'pred_logits' in outputs
src_logits = outputs['pred_logits'] #[bs, num_queries, num_classes]
idx = self._get_src_permutation_idx(indices) # 返回tuple,第一个值为图像索引,既哪个obj query对应哪张图像;第二个值为obj query索引
target_classes_o = torch.cat([t["labels"][J] for t, (_, J) in zip(targets, indices)]) # J为该图像对应的object索引,得到每个object对应的target labels
target_classes = torch.full(src_logits.shape[:2], self.num_classes,
dtype=torch.int64, device=src_logits.device) # [bs,num_queries]填满值为num_classes(此处为91)
target_classes[idx] = target_classes_o #此处表示在第i个image的第j个query填充对应的target_classes_o,此步骤为填充"no obj"
loss_ce = F.cross_entropy(src_logits.transpose(1, 2), target_classes, self.empty_weight) # [bs,num_query,num_classes] -> [bs,num_classes,num_query]
losses = {'loss_ce': loss_ce}
if log:
# TODO this should probably be a separate loss, not hacked in this one here
losses['class_error'] = 100 - accuracy(src_logits[idx], target_classes_o)[0] #错误个数
return losses
def _get_src_permutation_idx(self, indices):
# permute predictions following indices
batch_idx = torch.cat([torch.full_like(src, i) for i, (src, _) in enumerate(indices)]) # i为第i个图像,src为第i个图像对应的query的索引,_为第i个图像对应的object索引
# batch_idx得到[num_object],比如[0,0,1,1,1,1],可知哪个object对应哪个图像
src_idx = torch.cat([src for (src, _) in indices]) # 如tensor([22, 70, 7, 33, 34, 69]),既对应的object query索引
return batch_idx, src_idx

- box loss:
def loss_boxes(self, outputs, targets, indices, num_boxes):
"""Compute the losses related to the bounding boxes, the L1 regression loss and the GIoU loss
targets dicts must contain the key "boxes" containing a tensor of dim [nb_target_boxes, 4]
The target boxes are expected in format (center_x, center_y, w, h), normalized by the image size.
"""
assert 'pred_boxes' in outputs
idx = self._get_src_permutation_idx(indices)
src_boxes = outputs['pred_boxes'][idx] # [num_object,4]
target_boxes = torch.cat([t['boxes'][i] for t, (_, i) in zip(targets, indices)], dim=0) #[num_object,4]
loss_bbox = F.l1_loss(src_boxes, target_boxes, reduction='none')
losses = {}
losses['loss_bbox'] = loss_bbox.sum() / num_boxes
loss_giou = 1 - torch.diag(box_ops.generalized_box_iou(
box_ops.box_cxcywh_to_xyxy(src_boxes),
box_ops.box_cxcywh_to_xyxy(target_boxes)))
losses['loss_giou'] = loss_giou.sum() / num_boxes
return losses
2.4 其他
还会去计算辅助loss,可以提高训练速度以及稳定性。从源码中可以看到,CE Loss:L1 Loss: GIoU Loss = 1:5:2
3 DETR 模型
transformer模型架构如下:
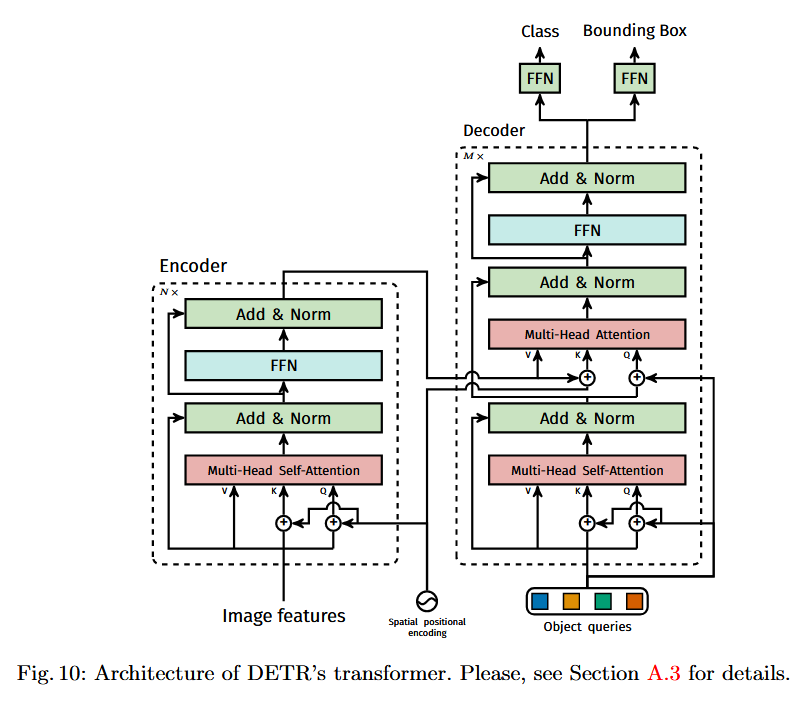
encoder输入的是image features,并且在Q、K位置上与spatial positional encoding相加,加入位置信息。经过6层encoder之后,输出带有全局相关性的image features,称作是memory(encoder output)
decoder的第一层输入是object query,先去做自注意力操作,随后的cross attention中,Q为decoder的输出,并且加上object query;K为memory,并且加上positional encoding,V为memory。object query可以表示为不同的objects(因为一个object query表示一个检测框),此处的注意力机制可以注入不同object的相关性,再加入到图像特征中。
如何构建就不分析了,主要就是backbone、positional encoding以及transformer,后面单独写文章去学习。主要看前向过程。但是注意object query的构建:
self.query_embed = nn.Embedding(num_queries, hidden_dim) 其实就是一个query embedding
3.1 前向过程
前向过程相较来说比较简单。
经过backbone,得到image features,尺寸为[bs,2048,h,w], 注意mask为[bs,h,w],mask表示哪个位置是被padding的,从而不计算其注意力。
随后将image features经过1x1卷积后,再变形为[hw,bs,256],同时将position embedding也变形为[hw,bs,256],并将query embedding变形为[100,bs,256]
送入到encoder,其中q和k要加上position embedding,v则不用。输出memory
def forward_post(self, src, src_mask: Optional[Tensor] = None, src_key_padding_mask: Optional[Tensor] = None, pos: Optional[Tensor] = None): q = k = self.with_pos_embed(src, pos) # 加上pos embedding src2 = self.self_attn(q, k, value=src, attn_mask=src_mask, key_padding_mask=src_key_padding_mask)[0] src = src + self.dropout1(src2) src = self.norm1(src) src2 = self.linear2(self.dropout(self.activation(self.linear1(src)))) src = src + self.dropout2(src2) src = self.norm2(src) return src送入到decoder中,其中做self-attention时,q和k都要加上query embedding,v则不用。做cross attention时,q则为tgt(decoder输出)和query embedding相加,k则为memory和positional embedding相加,v则为memory。
def forward_post(self, tgt, memory, tgt_mask: Optional[Tensor] = None, memory_mask: Optional[Tensor] = None, tgt_key_padding_mask: Optional[Tensor] = None, memory_key_padding_mask: Optional[Tensor] = None, pos: Optional[Tensor] = None, query_pos: Optional[Tensor] = None): q = k = self.with_pos_embed(tgt, query_pos) # 此处pos embedding为query pos tgt2 = self.self_attn(q, k, value=tgt, attn_mask=tgt_mask, key_padding_mask=tgt_key_padding_mask)[0] tgt = tgt + self.dropout1(tgt2) tgt = self.norm1(tgt) tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt, query_pos), key=self.with_pos_embed(memory, pos), value=memory, attn_mask=memory_mask, key_padding_mask=memory_key_padding_mask)[0] # self-attn和multihead_attn都是MultiHeadAttn tgt = tgt + self.dropout2(tgt2) tgt = self.norm2(tgt) tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt)))) tgt = tgt + self.dropout3(tgt2) tgt = self.norm3(tgt) return tgt最后的输出经过一层linear layer得到类别预测,经过MLP得到坐标预测(sigmoid)
4 实验结果

- 只关注encoder最后一层,关注几个点的位置,可见encoder似乎已经可以区分出不同的instances

- 对于decoder,由于encoder以及可以大致区分不同的instances,decoder更多是关注物体的极端
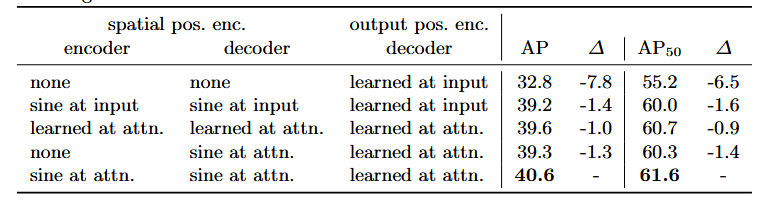
关于位置编码的消融:
如果只使用object query,AP下降非常多
如果只在第一层encoder和decoder使用positional encoding,则好很多,说明positional encoding很好使
如果使用learned positional encoding,并且在在整个传,会提升一点
如果不在encoder使用positional encoding,只在decoder的cross attention中使用,下降一点
第五行则是baseline
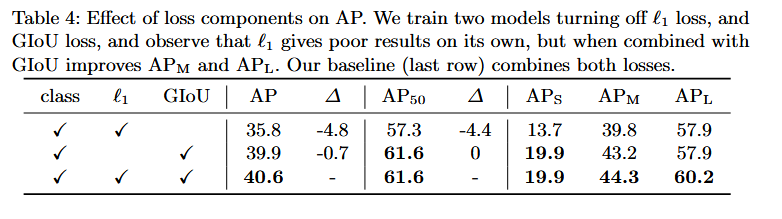
- 关于损失函数的消融

- 关于object query的可视化,虽然说看上去各司其职,但是重叠部分还是蛮大的