Deformable DETR

1 回顾DETR以及问题指出

1.1 DETR中transformer回顾

先来简单回顾一下DETR的transformer作用是什么:

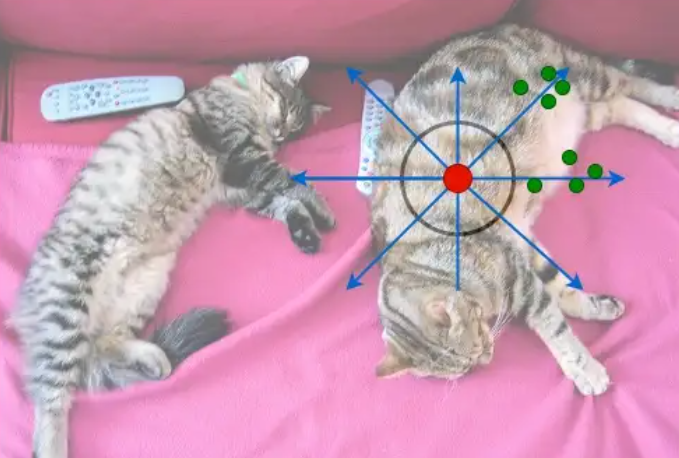
Encoder的输入是特征图的某个像素点向量（又叫token），通过self-attention，得到其与other tokens的相似度（similarity），通俗理解就是，位于🐱头的token理应和位于🐱jio的token相似度高，而与狗头或者牛马等不相同类别的物体的token相似度低。由下图的attention map可见，encoder的某一个token遍历其他所有token（包括自己）来学习自己应该关注哪些tokens，不该关注哪些tokens。可以说encoder的目的是掌握全局信息，是一种粗理解。
- 如何可视化attention map：计算出来的attention_weights有[H*W]个，reshape回 [H,W]，然后再按照attention_weights去高亮每个像素点就会得到attention map
Decoder的输入object query同样可以理解为特征图的某一个像素点，只不过它是随机的，这些像素点可以理解为检测框的质心。在训练过程中，这些质心不断调整自己的位置和区域，从而学习到自己应该关注的部分。由下图可知，每个object query学习的是自己应该关注的检测框的范围。

1.2 DETR两个重要问题

DETR存在两个重要问题：

（1）训练时间太长（300 epochs training on coco2017)

（2）难以检测小物体

已知transformer的计算公式为：

$$ Attn = \sum_{m=1}^M \{W_m [\sum_{k\in\Omega_k}exp(\frac{x_q^TW_q^TW_kx_k}{\sqrt{D_k}})]W_vx_v\} $$

如果$x_q:(N_q,C); W_q:(C,C)$，那么$Wq*x_q$的计算复杂度为$O(N_qC^2)$，所以我们可以得知attention的计算复杂度为$O(N_qC^2+N_kC^2+N_qN_kC)$，又$N_q=N_k>>C$,故最终的复杂度可以表示为$O(N_qN_kC)$

在DETR中，$N_q=N_k =H*W$,所以复杂度为$O(H^2W^2C)$,复杂度和特征图的面积成平方比例。而且这是个全局attention，一个token就必须和H*W个tokens做注意力计算，这也就预示着特征图的尺寸不能太大，而且也不能使用多尺度特征图（多个特征图），不然计算开销吃不消。且初始化时，Q和V遵循均值为0，方差为1的均匀分布

所以分子$exp(0) = 1, Attn =\frac{1}{N_k}$ ,因为$N_k$很大，所以Attn约等于0，会导致在训练初期的梯度随机，且需要很长时间才能让某一个token能关注到特殊的keys上。

而不能检测小物体通常是因为特征图尺寸不够大的问题，比如一个遥控器在某一个特征图上可能就一个点，一个点当然很难区分。若是可以用更大的特征图，遥控器的表达可能就是一个区域了。

2 Deformable DETR改进

针对以上两个问题，deformable提出两个改进方案：

（1）全局attention改为局部attention

（2）采用多尺度特征图

2.1 局部attention

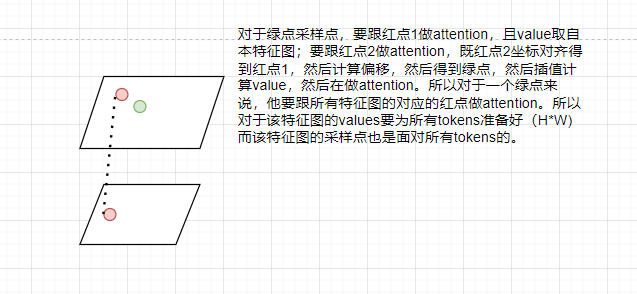
借鉴deformable convolution的思想，一个reference point（红点，也是token）只需要跟周围的sample points（绿点）做attention，这样可以加快收敛以及缓解特征图分辨率的问题。且理想情况也是，只需要关注物体周围的区域，就可以大致知道物体的shape以及label了。

既然如此，我们怎么规定reference points以及sample points呢？对于sample points，我们可以以reference points为中心的分8个方位（n_heads=8，约束方向），每个方向采样4个sample points（n_points=4），对于每个sample point，只要根据reference point去学习其偏移量（offsets），既可以由reference point和offsets得到sample points，然后该reference point和这些sample points去做注意力计算即可。模型不断学习update，改变周围的sample points的位置，这样的机制叫deformable attention。其实本质上这是限制其只与其周围像素点做attention的一种手段。不同的方向则有不同的head去构成。

2.2 单尺度deformable attention

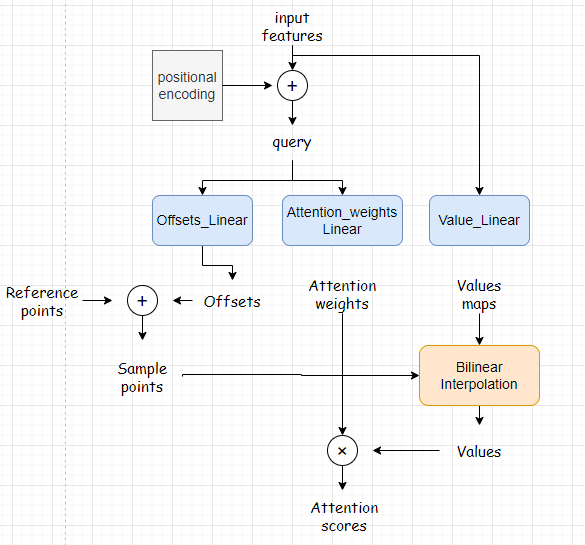
workflow如上图所示，input feature为backbone的输出，加上positional encoding之后变成query。这里设立三个FFN，其中一个通过input features生成value maps，其他两个通过query生成偏移以及attention weights（对的，此处的attention weights并不是通过$softmax(\frac{Q^TK}{\sqrt{d_k}})$计算得来）。reference points的实现源码稍后分析，总之根据reference points和offsets就可以得到sample points，然后通过插值的方法得到每个sample points的value（因为reference points很大可能是小数坐标），最后就可以得到attention scores了，忽略掉很多细节，看上去挺简单的。

计算公式为

$$ \text{DeformAttn}(z_q, p_q, x) = \sum_{m=1}^{M} W_m \left[ \sum_{k=1}^{K} A_{mqk} \cdot W'_m x (p_q + \Delta p_{mqk}) \right] $$

$K$表示采样点个数，远远小于$HW$, $x(.)$表示插值函数，此时计算复杂度变为$O(2N_qC^2+HWC^2)$

2.3 多尺度deformable attention

检测小物体的关键就是能运用多尺度的特征图。backbone resnet50中，取出C3、C4、C5的输出产出3种特征图，最后一个尺寸的特征图通过3x3卷积而来。一张图像将得到4张特征图（n_levels=4），其中前三种特征图通过1x1卷积降维，使之所有特征图的维度都相同（hidden_dim），这样得到的尺寸就分别是原图像宽高WH的1/8、1/16、1/32、1/64。

我们想做的是，对于每一张特征图的任意一个token，我们希望找到其在其他特征图的位置（坐标），这样除了在本特征图做deformable attention，还可以在其他尺寸特征图做deformable attention。最后通过某种方式，将各个尺度的attention结果综合起来。（所以我们只会知道一个特征图上的像素坐标，而不知道其他特征图的像素坐标？我们已知的特征图是C5吗？）

坐标对齐：

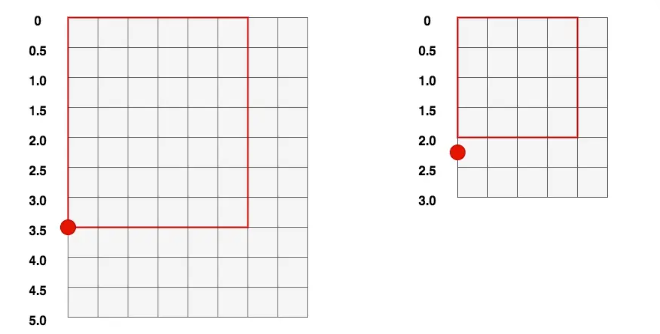
对于batch size大于1的情况，我们是会有padding操作的，而不同特征图之间的padding程度会不一样。那么我们就不可以用绝对坐标比例的方式取求得其他特征图的坐标：

由上面图举例可知，padding后左图1的3.5位置的比例为3.5/5.0=0.7；右图padding后0.7
比例位置的坐标为3.0*0.7=2.1，而3.5原来对应的是2.0才对。

我们用有效高度的方法来求得坐标：

设图1的高度H1，有效高度HE1，坐标p1； 图2的为2；
则我们可以知道p1/HE1 = p2/HE2, 所以得到 p1*HE2 / HE1 = p2;
此时除以H2，得p1/HE1 * HE2/H2 = p2/H2；
其中p1/HE1为图1的相对有效高度的坐标，HE2/H2为图二的有效高度比例；
这就可以得到图1的p1点，在图2的归一化的坐标。

这里还有一点需要注意的是，对于多尺度attention，我们除了加入2D位置编码，还会加入尺度层级位置编码（scale-level embedding）去区分像素query所在的特征图层数，该编码是随机初始化且可学习。

具体实现，会将不同的特征图的tokens展开成一排，作为attention的输入。（就是增加一维，大小为n_levels，然后展开酱紫）这样对于每一个head（方向）都需要学习 (n_levels, n_points)大小的attention weights, 最后将这几个attention weights一起做softmax。

对于一个token，我们可以得到其在自己特征图上的归一化坐标（既p1/HE1），然后用之前坐标对齐的方法去计算其他特征图的归一化坐标（乘上3个有效高度比例就得到3个特征图山上的归一化坐标表示），然后就可以在不同尺度下学习offsets，然后之后的操作就跟单尺度一样了。

3 全过程梳理

让我梳理一哈。

Images传入backbone得到4个input features,再reshape成符合transformer输入的形式（bs, HW, d_model）。这时候再与positional encoding相加则得到query（bs, HW, d_model），这里$H*W$表示所有的token数量，既4个特征图的所有tokens。

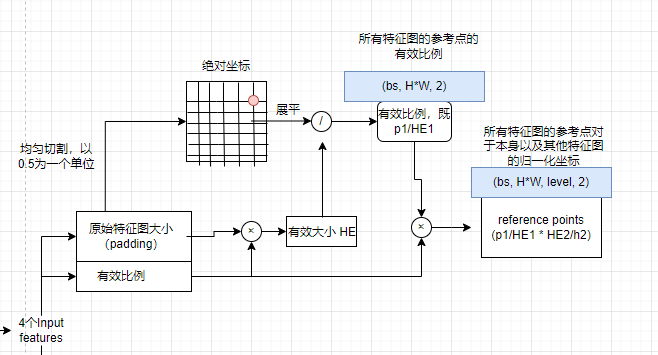
reference points初始化为对于每一张特征图，先按均匀分布在x和y方向切割，取其中心点。然后原始特征图大小乘上有效比例等于有效大小，然后中心点除以有效大小等于有效比例，既$p1/HE1$。最后在第1维concat，得到尺寸(bs, H*W, 2)，表示所有特征图的reference points的有效比例。最后乘以valid_ratios，得到reference_points，尺寸为（bs, H *W, level, 2) ，表示对于所有特征图的reference points，其在该特征图以及其他特征图的归一化坐标。

sample_offset、value_proj、attention_weights都是Linear layers，特别注意的是对于偏移量的初始化：

设置8个方向的thetas 【0, pi/4, … 7pi/4】，此时shape为（8，）
设置8个方向的正余弦 grid_init，此时shape为（8，2）
将正余弦转换为米字，代码和展示如下，就得到【(1,0),(1,1),…(1,-1)】
进行尺度变换为(8,4,4,2),对应(head,level,point,2)，此时同一个方向采样点的偏移都是一样的，对其进行区分，使得第一个采样点为(1,0),(1,1)…，第二个采样点为(2,0),(2,2)..等

最后就跟单尺度deformable attention展示的一样。需要注意的是最后的插值采样：

细品。

def ms_deform_attn_core_pytorch(value, value_spatial_shapes, sampling_locations, attention_weights):
    """
    Args:
        value: 尺寸为：(B, sum(所有特征图的token数量), nheads, d_model//n_heads)。对原始token做线性变化
               后的value值
        input_spatial_shapes: tensor，其尺寸为(level_num，2)。 表示原始特征图的大小。
                              其中2表是Hi, Wi。例如：
                              tensor([[94, 86],
                                      [47, 43],
                                      [24, 22],
                                      [12, 11]])
        sampling_locations：尺寸为(B, sum(tokens数量), nhead, n_levels, n_points, 2)。
                            每个token在每个head、level上的n_points个偏移点坐标(坐标是归一化的像素值),
                            每个坐标是按(w,h)表达的，注意不是(h,1)

        attention_weights: 尺寸为(B, sum(tokens数量), nheads, n_levels, n_points)
                           每个token在每个head、level上对n_points个偏移点坐标的注意力权重
    """
    # for debug and test only,
    # need to use cuda version instead
    N_, S_, M_, D_ = value.shape
    _, Lq_, M_, L_, P_, _ = sampling_locations.shape
    value_list = value.split([H_ * W_ for H_, W_ in value_spatial_shapes], dim=1)  # 将value按照特征图进行split,得到长度为(level)的tuple,每一个值为(bs,H_*W_,head,head_dim)
                                                                                   # H_*W_表示某一个特征图的大小，head把个头，head_dim表示一个value为长度head_dim的向量
    sampling_grids = 2 * sampling_locations - 1 # 将采样点从(0,1)变成(-1,1)，方便插值计算
    sampling_value_list = []
    for lid_, (H_, W_) in enumerate(value_spatial_shapes):  # 遍历每一个特征图 
        value_l_ = value_list[lid_].flatten(2).transpose(1, 2).reshape(N_*M_, D_, H_, W_) # 取出当前特征图的value，变换尺寸为(bs*head, head_dim, h_, w_),可以理解为将每个value map展平
                                                                           
        sampling_grid_l_ = sampling_grids[:, :, :, lid_].transpose(1, 2).flatten(0, 1) # 取出当前特征图的采样点，变换尺寸为(bs*head, H*W, point, 2)
                                                                                    # 重点理解一下，每个tokens（所有特征图）在当前特征图每个方向的采样点，因为一个特征图的采样点要和
                                                                                    # 所有特征图该位置的tokens做attention
        sampling_value_l_ = F.grid_sample(value_l_, sampling_grid_l_,
                                          mode='bilinear', padding_mode='zeros', align_corners=False)   # (bs*head, head_dim, H*W, point),所有tokens对于该特征图的采样点的values
        sampling_value_list.append(sampling_value_l_)
        # 这是比较难理解的，一个token会坐标对齐找到其他特征图的tokens'的归一化坐标，然后该tokens'在做偏移，然后插值得到values，此时的token会跟该采样点做attention，用的就是这个values
    
    attention_weights = attention_weights.transpose(1, 2).reshape(N_*M_, 1, Lq_, L_*P_) # (bs, H*W, head, level, point) -> (bs*head, 1, H*W, level*point)
    output = (torch.stack(sampling_value_list, dim=-2).flatten(-2) * attention_weights).sum(-1).view(N_, M_*D_, Lq_)    #stack\flatten之后 (bs*head, head_dim, H*W, level*points)
                                                                                                                    # ×之后,(bs*head, head_dim, H*W, level*point)
                                                                                                                    # 求和 (bs*head, head_dim, H*W)
                                                                                                                    # view (bs, head*head_dim, H*W)
    return output.transpose(1, 2).contiguous()  # (bs, H*W, d_model)

1 回顾DETR以及问题指出#

1.1 DETR中transformer回顾#

1.2 DETR两个重要问题#

2 Deformable DETR改进#

2.1 局部attention#

2.2 单尺度deformable attention#

2.3 多尺度deformable attention#

3 全过程梳理#